Ya hemos mencionado en una entrada anterior que teníamos intención de estudiar los Grandes Cardinales. Y en otro rincón del blog avisabamos cuales especies de Grandes Cardinales nos interesaban para este blog. Empezaremos por los más digeribles, que son los pequeños.
En otra entrada definiremos el universo L construible de Gödel, pero mientras tanto podemos afirmar que un gran cardinal pequeño cumple con que su axioma de grande cardinal sea consistente con el universo L. En otras palabras, si es consistente con V entonces es consistente con L.
Si el condicional de arriba no se satisface, entonces el gran cardinal no era pequeño sino grande.
Estos cardinales pequeños no son nada más que cardinales límite. Pero se dividen en dos tipos: los débiles y los fuertes.
Aquellos que son débiles, son aquellos que no podemos llegar con operaciones de sucesor, precisamente porque son límite y no hay un antecesor directo.
Los que son fuertes son aquellos que ni siquiera podemos llegar con operaciones de conjunto partes, para todo cardinal κ < λ se tiene que 2κ < λ, pues ni siquiera sacar partes será suficiente para rebasar λ. Sea κ+ el sucesor de κ, para estos siempre se tiene que κ+ ≤ 2κ pero como 2κ < λ entonces κ+< λ para todo κ por lo que los fuertes son particularmente débiles, pues tampoco se pueden alcanzar con operaciones sucesor.
Por supuesto que existe un método para hallar varios cardinales límite, lo mostramos, es una inducción transfinita.
El primer cardinal límite:

Acá, la cardinalidad de un sucesor es la cardinalidad del conjunto partes del anterior:

Y, tan similar al universo V que construimos, para ordinales límite λ, como ω, tenemos:
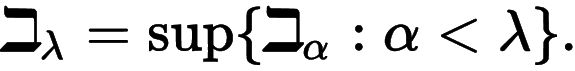
A ese símbolo que es tal vez nuevo lo llamamos beth y ahí mismo definimos como funciona la operación beth. Beth es la segunda letra hebrea.
Cada cardinal beth es un cardinal límite fuerte, y pues viene sin tanto lío saber que es débil también.
Jech, Thomas (2003), Set Theory, Springer Monographs in Mathematics (third millennium ed.), Berlin, New York: Springer-Verlag, doi:10.1007/3-540-44761-X, ISBN 978-3-540-44085-7